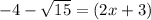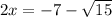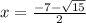Answer:
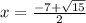
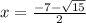
Step-by-step explanation:
we have
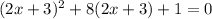
Let
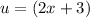
substitute the variable
so
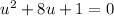
we know that
The formula to solve a quadratic equation of the form
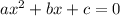
is equal to
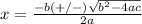
in this problem we have
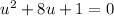
so
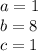
substitute in the formula
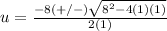
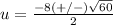
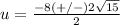
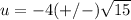
so
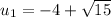
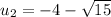
Find the value of x
Remember that
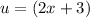
First solution
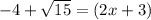
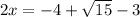
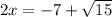
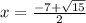
Second solution