Question

The Pew Internet and American Life Project reported Wednesday, April 18th that two- thirds (67%) of young adults with profiles on social-networking sites have restricted access to their profiles by requiring passwords or making them available only to friends on an approved list ("Study: Teens protecting their profiles" POSTED: 10:54 a.m. EDT, April 19, 2007 on CNN.com). A researcher believes that military personnel are more careful with keeping themselves safe online and surveys a random sample of 100 enlisted military personnel students and finds that 78 students restrict access to their profiles. Does this indicate at the 5% significance level that a larger proportion of military personnel protect their profiles on social-networking sites?

Answer 1

At 5% significance level, larger proportion of military personnel students protect their profiles on social-networking sites than young adults with profiles on social-networking sites.

Explanation:

let p be the proportion of military personnel students who restrict access to their profiles. Then null and alternative hypotheses are:

`H_(0)`: p=0.67 (67%)

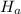`H_(a)`: p>0.67

We need to calculate z-statistic of sample proportion:

z=
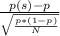`\frac{p(s)-p}{\sqrt{(p*(1-p))/(N) } }` where

• p(s) is the sample proportion of military students who restrict access to their profiles (
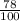  `(78)/(100)` =0.78)

• p is the proportion assumed under null hypothesis. (0.67)

• N is the sample size (100)

Then z=
`\frac{0.78-0.67}{\sqrt{(0.67*0.33)/(100) } }` ≈ 2.34

The corresponding p-value is 0.0096. Since 0.0096<0.05 (significance level) we can reject the null hypothesis and conclude at 5% significance level that larger proportion of military personnel students protect their profiles on social-networking sites than young adults with profiles on social-networking sites.