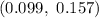Answer:
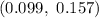
Explanation:
We know that the confidence interval for population standard deviation is given by :-
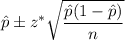
, where , n= sample size.
 = sample proprotion.
= sample proprotion.
z* = critical z-value.
Given : A random sample of 500 registrations are selected from a Department of Motor Vehicles database, and 64 are classified as sports utility vehicles.
i.e. n= 500

We know that critical z-value for 95% confidence = z*=1.96
Then, the 95% confidence interval to estimate the proportion of sports utility vehicles in California will be :-
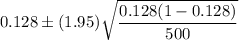
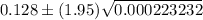
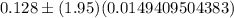
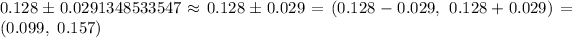
Hence, the 95% confidence interval to estimate the proportion of sports utility vehicles in California. =