Answer:
Both end hinge-Pcr= 0.98 MN
Both end fix-Pcr=3.9 MN
Step-by-step explanation:
E= 200 GPa
L=2 m
b=7 cm =70 mm
The critical load given as
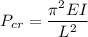
For square section
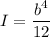

Lets take column is hinge at the both ends :
Now by putting all the values

L'= L
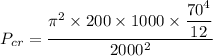
Pcr=987371.6 N
Pcr= 0.98 MN
Therefore critical load = 0.98 MN
When both end fixed :

L' = 0.5 L
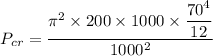
Pcr=3.9 MN
Therefore critical load = 3.9 MN