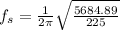Question

A uniform beam is suspended horizontally by two identical vertical springs that are attached between the ceiling and each end of the beam. The beam has mass 225 kg, and a 175-kg sack of gravel sits on the middle of it. The beam is oscillating in SHM, with an amplitude of 40.0 cm and a frequency of 0.600cycles/s. Part A The sack of gravel falls off the beam when the beam has its maximum upward displacement. What is the frequency of the subsequent SHM of the beam?

Answer 1

The frequency as calculated is 0.79 Hz

Solution:

As per the question:

Mass of the beam, m = 225 kg

Mass of the sack, m' = 175 kg

Amplitude, A = 40.0 cm = 0.4 m

Frequency, f = 0.6 Hz

Now,

(A) To calculate the frequency of the SHM:

The total mass, M = m + m' = 225 + 175 = 400 kg

With the help of the eqn:

`f = (1)/(2\pi)\sqrt{(k)/(M)}`

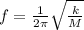
where

k = spring constant

Thus

`0.6 = (1)/(2\pi)\sqrt{(k)/(400)}`

`0.6* 2\pi * 20 = √(k)`

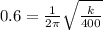
Squaring both sides, we get:

k = 5684.89 N/m

Now, after the gravel has fallen:

m = 275 kg

Now,

The frequency of the SHM can be calculated as:

`f_(s) = (1)/(2\pi)\sqrt{(5684.89)/(225)}`

`f_(s) = 0.79\ Hz`