Answer:
The frequency as calculated is 0.79 Hz
Solution:
As per the question:
Mass of the beam, m = 225 kg
Mass of the sack, m' = 175 kg
Amplitude, A = 40.0 cm = 0.4 m
Frequency, f = 0.6 Hz
Now,
(A) To calculate the frequency of the SHM:
The total mass, M = m + m' = 225 + 175 = 400 kg
With the help of the eqn:
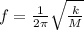
where
k = spring constant
Thus
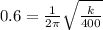

Squaring both sides, we get:
k = 5684.89 N/m
Now, after the gravel has fallen:
m = 275 kg
Now,
The frequency of the SHM can be calculated as:

