Question

Consider two consecutive positive integers such that the square of the second integer added to 3 times the first is equal to 85

Answer 1

The Two Consecutive integers are 7 and 8.

Explanation:

Let the first Integer be x

Since the two numbers are consecutive

therefore the second number will be x+1

Now given:

the square of the second integer added to 3 times the first is equal to 85

Hence framing the above sentence in mathematical form we get;

`(x+1)^2+3x=85`

Now Solving the above equation we get;

since
`(a+b)^2 = a^2+2ab+b^2`

`x^2+2x+1+3x=85`

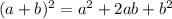
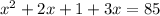
Using addition property we get;

`x^2+5x+1-85=0`

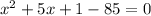
Using Subtraction property we get;

`x^2+5x-84=0`

Now factorizing above equation we get;

`x^2+12x-7x-84=0\\x(x+12)-7(x+12)=0\\(x-7)(x+12)=0\\x-7=0 \ \ \ \ \ \ \ \ or \ \ \ \ \ \ x+12 = 0\\x= 7\ \ \ \ \ \ \ \ or \ \ \ \ \ \ \ \ x=-12`

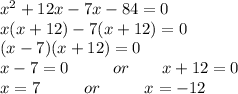
Now we get 2 values of x which is 7 and -12.

Since it is given that number is positive Integer hence the number will be 7

and the other number would 7 + 1 = 8.