Answer:
The Two Consecutive integers are 7 and 8.
Explanation:
Let the first Integer be x
Since the two numbers are consecutive
therefore the second number will be x+1
Now given:
the square of the second integer added to 3 times the first is equal to 85
Hence framing the above sentence in mathematical form we get;
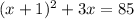
Now Solving the above equation we get;
since
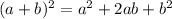
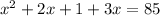
Using addition property we get;
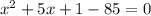
Using Subtraction property we get;
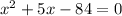
Now factorizing above equation we get;
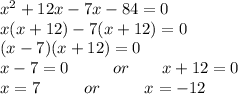
Now we get 2 values of x which is 7 and -12.
Since it is given that number is positive Integer hence the number will be 7
and the other number would 7 + 1 = 8.