Answer:
Chi-Square value for lower bond: X²
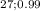 = 46963
= 46963
Chi-Square value for upper bond: X²
 = 12.878
= 12.878
Confidence interval: [0.0278;0.1001]
Explanation:
Hello!
You need to make a 98% Confidence interval for the population variance of a single sample. To construct it you have to use a Chi-Square statistic:
X²= (n-1)S² ~X²

σ²
The formula for the interval is:
Lower bond:
(n-1)S² = 27*0.0484 = 1.3068 = 0.0278
X²
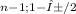 X²
X²
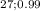 46.963
46.963
Upper bond:
(n-1)S² = 2*0.0484 = 1.3068 = 0.1001
X²
 X²
X²
 12.878
12.878
n=28
S= 0.22
S²=0.0484
With a 98% confidence level, you'd expect the true value of the nicotine variance in menthol cigarettes is contained by the interval [0.0278;0.1001]
I hope it helps!