Question

Imagine an experiment having three conditions and 20 subjects within each condition. The mean and variances of each condition are listed below.

Condition Mean Variance
Condition 1 3.2 14.3
Condition 2 4.2 17.2
Condition 3 7.6 16.7
1. What’s the valueof mean squares between groups (MSB)?
2.What’s the value of mean square error (MSE)?
3. Whats the value of F?
4. What’s the probability value of this result?

Answer 1

1. Mean square B= 5.32

2. Mean square E= 16.067

3. F= 0.33

4. p-value: 0.28

Explanation:

Hello!

You have the information of 3 groups of people.

Group 1

n₁= 20

X[bar]₁= 3.2

S₁²= 14.3

Group 2

n₂= 20

X[bar]₂= 4.2

S₂²= 17.2

Group 3

n₃= 20

X[bar]₃= 7.6

S₃²= 16.7

1. To manually calculate the mean square between the groups you have to calculate the sum of square between conditions and divide it by the degrees of freedom.

Df B= k-1 = 3-1= 2

Sum Square B is:

∑ni(Ÿi - Ÿ..)²

Ÿi= sample mean of sample i ∀ i= 1,2,3

Ÿ..= general mean is the mean that results of all the groups together.

General mean:

Ÿ..= (Ÿ₁ + Ÿ₂ + Ÿ₃)/ 3 = (3.2+4.2+7.6)/3 = 5

Sum Square B (Ÿ₁ - Ÿ..)² + (Ÿ₂ - Ÿ..)² + (Ÿ₃ - Ÿ..)²= (3.2 - 5)² + (4.2 - 5)² + (7.6 - 5)²= 10.64

Mean square B= Sum Square B/Df B= 10.64/2= 5.32

2. The mean square error (MSE) is the estimation of the variance error (σ
`_(e)^2` →
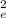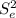`S_(e) ^(2)`), you have to use the following formula:

Se²= (n₁-1)S₁² + -(n₂-1)S₂² + (n₃-1)S₃²

n₁+n₂+n₃-k

Se²= 19*14.3 + 19*17.2 + 19*16.7 = 915.8 = 16.067

20+20+20-3 57

DfE= N-k = 60-3= 57

3. To calculate the value of the statistic you have to divide the MSB by MSE

`F= (Mean square B)/(Mean square E) = (5.32)/(16.067) = 0.33`

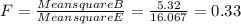
4. P(F
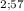`_(2; 57)` ≤ F) = P(F
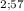`_(2; 57)` ≤ 0.33) = 0.28

I hope you have a SUPER day!