Answer:
1. Mean square B= 5.32
2. Mean square E= 16.067
3. F= 0.33
4. p-value: 0.28
Explanation:
Hello!
You have the information of 3 groups of people.
Group 1
n₁= 20
X[bar]₁= 3.2
S₁²= 14.3
Group 2
n₂= 20
X[bar]₂= 4.2
S₂²= 17.2
Group 3
n₃= 20
X[bar]₃= 7.6
S₃²= 16.7
1. To manually calculate the mean square between the groups you have to calculate the sum of square between conditions and divide it by the degrees of freedom.
Df B= k-1 = 3-1= 2
Sum Square B is:
∑ni(Ÿi - Ÿ..)²
Ÿi= sample mean of sample i ∀ i= 1,2,3
Ÿ..= general mean is the mean that results of all the groups together.
General mean:
Ÿ..= (Ÿ₁ + Ÿ₂ + Ÿ₃)/ 3 = (3.2+4.2+7.6)/3 = 5
Sum Square B (Ÿ₁ - Ÿ..)² + (Ÿ₂ - Ÿ..)² + (Ÿ₃ - Ÿ..)²= (3.2 - 5)² + (4.2 - 5)² + (7.6 - 5)²= 10.64
Mean square B= Sum Square B/Df B= 10.64/2= 5.32
2. The mean square error (MSE) is the estimation of the variance error (σ
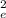 →
→
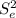 ), you have to use the following formula:
), you have to use the following formula:
Se²= (n₁-1)S₁² + -(n₂-1)S₂² + (n₃-1)S₃²
n₁+n₂+n₃-k
Se²= 19*14.3 + 19*17.2 + 19*16.7 = 915.8 = 16.067
20+20+20-3 57
DfE= N-k = 60-3= 57
3. To calculate the value of the statistic you have to divide the MSB by MSE
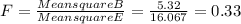
4. P(F
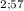 ≤ F) = P(F
≤ F) = P(F
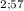 ≤ 0.33) = 0.28
≤ 0.33) = 0.28
I hope you have a SUPER day!