Question

An isentropic steam turbine processes 2 kg/s of steam at 3 MPa, which is exhausted at50 kPa and 100C. Five percent of this flow is delivered for feedwater heating at 500 kPa. Determine the power produced by this turbine, in kW.

Answer 1

2285kw

Step-by-step explanation:

since it is an isentropic process, we can conclude that it is a reversible adiabatic process. Hence the energy must be conserve i.e the total inflow of energy must be equal to the total outflow of energy.

Mathematically,

`\\ E_(inflow) = E_(outflow)`

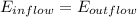
Note: from the question we have only one source of inflow and two source of outflow (the exhaust at a pressure of 50kpa and the feedwater at a pressure of 5ookpa). Also the power produce is another source of outgoing energy
`\\ E_(inflow) = m_(1) h_(1)` .

`\\`

`E_(outflow) = m_(2) h_(2) + m_(3) h_(3) + W_(out)`

`\\`

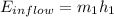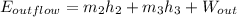
Where
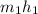`m_(1) h_(1)` are the mass flow rate and the enthalpies at the inlet at a pressure of 3Mpa
`\\`,

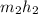`m_(2) h_(2)` are the mass flow rate and the enthalpies at the outlet 2 where we have a pressure of 500kpa respectively.
`\\`,

and
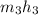`m_(3) h_(3)` are the mass flow rate and the enthalpies at the outlet 3 where we have a pressure of 50kpa respectively.
`\\`,

We can now express write out the required equation by substituting the new expression for the energies
`\\`

`m_(1) h_(1) = m_(2) h_(2) + m_(3) h_(3) + W_(out)`
`\\`

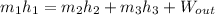
from the above equation, the unknown are the enthalpy values and the mass flow rate.
`\\`

first let us determine the enthalpy values at the inlet and the out let using the Superheated water table.
`\\`

It is more convenient to start from outlet 3 were we have a temperature
`100^(0)C` and pressure value of (50kpa or 0.05Mpa ). using double interpolation method on the superheated water table to determine the enthalpy value with careful calculation we have
`\\`

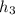`h_(3)` = 2682.4 KJ/KG , at this point also from the table the entropy value ,
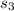`s_(3)` value is 7.6953 KJ/Kg.K.
`\\`

Next we determine the enthalphy value at outlet 2. But in this case, we don't have a temperature value, hence we use the entrophy value since the entropy is constant at all inlet and outlet.
`\\`

So, from the superheated water table again, at a pressure of 500kpa (0.5Mpa) and entropy value of 7.6953 KJ/Kg.K with careful interpolation we arrive at a enthalpy value of 3206.5KJ/Kg.
`\\`

Finally for inlet one at a pressure of 3Mpa, interpolting with an entropy value of 7.6953KJ/Kg.K we arrive at enthalpy value of 3851.2KJ/Kg.
`\\`

Now we determine the mass flow rate at each inlet and outlet. since mass must also be balance, i.e
`m_(1) = m_(2) + m_(3)`
`\\`

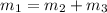
From the question the, the mass flow rate at the inlet
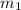`m_(1)}` is 2Kg/s
`\\`

Since 5% flow is delivered into the feedwater heating,
`\\`

`m_(2) = 0.05m_(1) = 0.05 *2kg/s = 0.1kg/s`
`\\`

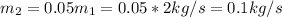
Also for the outlet 3 the remaining 95% will flow out. Hence

`m_(3) = 0.95m_(1) = 0.95 *2kg/s = 1.9kg/s`
`\\`

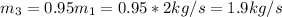
Now, from
`m_(1) h_(1) = m_(2) h_(2) + m_(3) h_(3) + W_(out)`
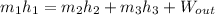
`\\` we substitute values

`W_(out) = m_(1) h_(1)-m_(2) h_(2)-m_(3) h_(3)`

`W_(out) = (2kg/s)(3851.2KJ/Kg) - (0.1kg/s)(3206.5kJ/kg)- (1.9)(2682.4kJ/kg)`

`\\`

`W_(out) = 2285.19 kW`.

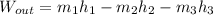
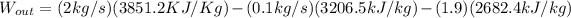
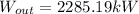Hence the power produced is 2285kW