Answer:
OPTION D
Explanation:
We have to determine which option determines the function given above.
To determine the function, just substitute the values and compare LHS and RHS.
we have
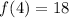
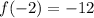
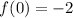
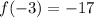
Here,
 is the domain and
is the domain and
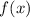 is the co-doamin.
is the co-doamin.
Therefore,
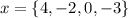
Now, OPTION A:
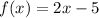
Substitute x = 4. We get f(x) = 3
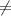 18.
18.
So, OPTION A is rejected.
Similarly, OPTION B:
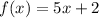
Substitute x = 4. We get f(4) = 22
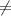 18.
18.
It is rejected as well.
Now, for OPTION C:
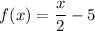
Substitute x = 4. We get f(4) = -3
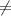 18.
18.
So, OPTION C is also rejected.
OPTION D:
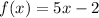
Substitute x = 4. We get f(4) = 18.
Substitute the remaining points in domain as well. We notice that it exactly matches the given function. So, OPTION D is the answer.