Answer:
If
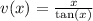 , then
, then
 is even.
is even.
If
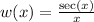 , then
, then
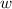 is odd.
is odd.
Explanation:
Summary of rules/ what we need:
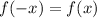 implies
implies
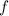 is even.
is even.
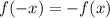 implies
implies
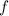 is odd.
is odd.
So in either case, we need to replace
 with
with
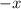 .
.
Let's begin.
First Problem:
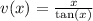
Replace
 with
with
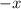 :
:
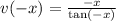
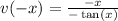 (We used
(We used
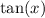 is odd; that is,
is odd; that is,
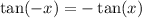 )
)
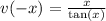
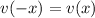
This implies
 is an even function.
is an even function.
Second Problem:
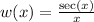
Replace
 with
with
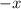 :
:
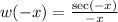
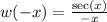 (We used
(We used
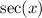 is even; that is,
is even; that is,
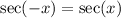 )
)
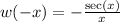
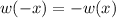
This implies
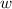 is an odd function.
is an odd function.