Question

The marginal price per pound (in dollars) at which a coffee store is willing to supply x pounds of Jamaican Blue Mountain coffee per week is given by p ′ (x) = 208 (x + 7)2 . If the coffee shop is willing to supply 9 pounds per week at a price of $7 per pound, determine how many pounds it would be willing to supply at a price of $4 per pound?

Answer 1

Thus, the coffee shop is willing to supply 6 pounds per week at a price of $4 per pound.

Explanation:

We are given the following information in the question:

The marginal price per pound (in dollars) is given by:

`p'(x) = \displaystyle(208)/((x+7)^2)`

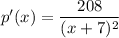
where x is the supply in pounds.

`P(x) = \displaystyle\int p'(x)~dx =\displaystyle\int\displaystyle(208)/((x+7)^2)~dx\\\\P(x) = (-208)/((x+7)) + c\\\\\text{where c is the constant of integration.}`

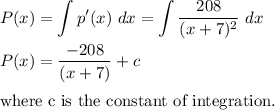
The coffee shop is willing to supply 9 pounds per week at a price of $7 per pound.

Thus, we are given that

P(9) = 7

Putting the values, we get,

`P(x) = \displaystyle(-208)/((x+7)) + c\\\\P(9) = 7\\\\\displaystyle(-208)/((9+7)) + c = 7\\\\c = 7 + (208)/(16) = 20`

`P(x) = \displaystyle(-208)/((x+7)) + 20`

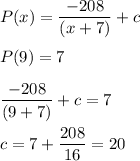
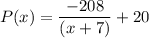
Now, we have to find how many pounds it would be willing to supply at a price of $4 per pound.

P(x) = 4

`P(x) = \displaystyle(-208)/((x+7)) + 20 = 4\\\\(-208)/(x+7) = -16\\\\x + 7 = 13\\x = 6`

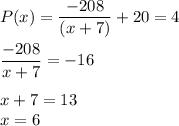
Thus, the coffee shop is willing to supply 6 pounds per week at a price of $4 per pound.