Question

Length of the fence of a trapezium shaped field ABCD is 120meter.If BC=48m,CD=17m and AD=40m,find te area of this field.Sde AB is perpendicular to the parallel side AD and BC

Answer 1

The area of the field is
`660 m^(2)`

Explanation:

Given that the measurements are

AD = 40 m, CD = 17 m, BC = 48 m

In the given figure, construct Line perpendicular from D to side CB.

So the formed figure is rectangle and triangle.

The triangle being right angled, applying pythagoras theorm ,

`17^(2) = 8^(2) + x^(2)`

Thus,
`x^(2) = 289 - 64 = 225`

`x = 15 m`

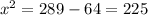
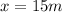
thus, AB = 15 m ( rectangle opposite sides are equal)

Thus, Area of trapezium is,

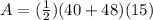
`A = ((1)/(2))(Sum of parralle sides)(distance between them)`

`A = ((1)/(2))(40 + 48)(15)`

A =
`660 m^(2)`