Answer:
3.60342 seconds
Step-by-step explanation:
v = Initial velocity of snowball = 25 m/s
g = Acceleration due to gravity = 9.81 m/s²
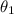 = First angle = 75°
= First angle = 75°
The second angle will be

Horizontal speed for first throw
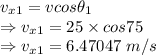
Horizontal speed for second throw

Horizontal range is given by
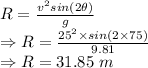
Time period for first throw
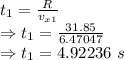
Time period for second throw
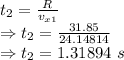
The time difference is
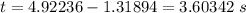
The second ball should be thrown 3.60342 seconds later