Answer:
a)
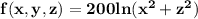
b)
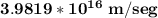
Explanation:
The electric field can be written as
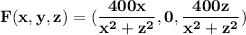
a)Find a potential function for F
A potential function for F would be a function f such that
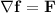
That is, the gradient of f equals F.
If such a function exists then
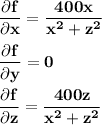
Integrating the first equation with respect to x
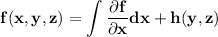
where h(y,z) is a function that does not depend on x. We have then
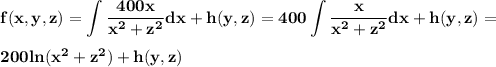
By taking the partial derivatives with respect y and z we can notice that h(z,y)=0.
Therefore, a potential function for F is

b) What is the electron’s speed at the point Q?
Since F is conservative, the work done to move the particle from P to Q does not depend on the path, but only on the potential function f.
Let W be the work done when moving the particle from P to Q
W = f(Q) - f(P) = f(1,1,1) - f(5,3,7)
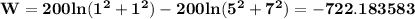 joules
joules
According to the law of conservation of energy, the work done to move the electron from P to Q equals the change in kinetic energy of the object.
Since the electron is at rest in P, the kinetic energy at P equals 0 and we have
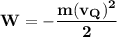
where
m = mass of an electron
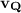 = speed at point Q
= speed at point Q
Replacing in the equation
