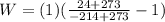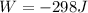Question

How much work must be done by a Carnot refrigerator to transfer 1.00 J as heat (a) from a reservoir at 8.40°C to one at 24.0°C, (b) from a reservoir at -78.0°C to one at 24.0°C, (c) from a reservoir at -153°C to one at 24.0°C, and (d) from a reservoir at -214°C to one at 24.0°C

Answer 1

To solve this problem it is necessary to apply the concepts related to the coefficient of performance (COP) of a heat pump, cooling or an air conditioning system. Said performance coefficient basically expresses the radius of useful heating or cooling provided to work required. At this case we use the expression for a Refrigerator.

Mathematically it can be expressed as

`COP = (Q_H)/(W) \Rightarrow COP = (T_C)/(T_H-T_C)`

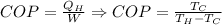
Where

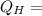`Q_H =`Heat of hot reservoir

W = Work

`T_H =` Temperature of hot reservoir

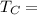`T_C =`Temperature of cold reservoir

Matching the two equations we have to

`(Q_H)/(W) = (T_C)/(T_H-T_C)`

Re-arrange to find the Work

`W = Q_H(T_H-T_C)/(T_C)`

`W = Q_H((T_H)/(T_C)-1)`

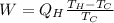
Our values depend on each point but for all the heat that is equivalent to 1 remains the same, therefore replacing for each one,

PART A)

`W = Q_H((T_H)/(T_C)-1)`

`W = (1)((24+273)/(8.4+273)-1)`

`W = 0.05543J`

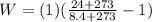
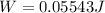
PART B)

`W = Q_H((T_H)/(T_C)-1)`

`W = (1)((24+273)/(-78+273)-1)`

`W = 0.523J`

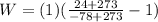
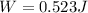
PART C)

`W = Q_H((T_H)/(T_C)-1)`

`W = (1)((24+273)/(-153+273)-1)`

`W = 1.475J`

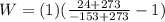
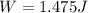
PART D)

`W = Q_H((T_H)/(T_C)-1)`

`W = (1)((24+273)/(-214+273)-1)`

`W = -298J`