Step-by-step explanation:
In order to find the net electric field, we have to find the four electric fields and add them as vecotrs.
Hence, formula to calculate the electric field is as follows.
E =
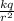
For the charge at x = 0.042 m (as 1 m = 100 cm)
So,
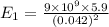
=
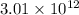 N (toward the negative x direction)
N (toward the negative x direction)
For the charge at x = -0.042 m
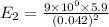
=
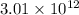 N (toward the positive x direction)
N (toward the positive x direction)
For the charge at y = 0.048 m
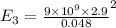
=
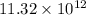 N (toward the negative y direction)
N (toward the negative y direction)
For the charge at y = 0.069 m
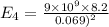
=
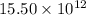 N (toward the positive y)
N (toward the positive y)
Therefore, net x is calculated as follows.
The net x =
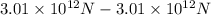
= 0 N
The net y =
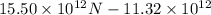 N
N
=
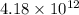 N (positive y)
N (positive y)
Total net E is found by the pythagorean theorem as follows.
E =
![\sqrt{[(0 N)^(2) + (4.18 * 10^(12) N)^(2)]](https://img.qammunity.org/2020/formulas/physics/high-school/r2q1v042tpbojqmzew0r08c9eae79b65e5.png)
=
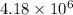 N
N
Thus, we can conclude that the net electric field (magnitude and direction) at the origin is
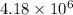 N.
N.