Question

Two point charges are located along the x axis: q1 = +5.9 μC at x1 = +4.2 cm, and q2 = +5.9 μC at x2 = −4.2 cm. Two other charges are located on the y axis: q3 = +2.9 μC at y3 = +4.8 cm, and q4 = −8.2 μC at y4 = +6.9 cm. Find the net electric field (magnitude and direction) at the origin.

Answer 1

Step-by-step explanation:

Given

`q_1=+5.9\mu C`

`q_2=+5.9\mu C`

`q_3=+2.9\mu C`

`q_4=-8.2\mu C`

Electric field is given by

`E=(kq)/(r^2)`

Electric field due to
`q_1` and
`q_2` cancel out each other because they point in opposite direction in x-axis

so net Electric field will be because of
`q_3` and
`q_4` towards negative Y axis

`E_3=(kq_3)/(r_3^2)`

`E_3=(9* 10^9* 2.9* 10^(-6))/((4.8* 10^(-2))^2)`

`E_3=1.132* 10^7`(away from q_3[/tex])

similarly
`E_4=1.55* 10^(7)` (towards q_4[/tex])

`E_(net)=E_4-E_3=1.55* 10^(7)-1.132* 10^7`

`E_(net)=0.41* 10^7 N/C`

Answer 2

Step-by-step explanation:

In order to find the net electric field, we have to find the four electric fields and add them as vecotrs.

Hence, formula to calculate the electric field is as follows.

E =
`(kq)/(r^(2))`

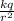
For the charge at x = 0.042 m (as 1 m = 100 cm)

So,
`E_(1) = (9 * 10^(9) * 5.9)/((0.042)^(2))`

=
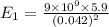
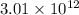`3.01 * 10^(12)` N (toward the negative x direction)

For the charge at x = -0.042 m

`E_(2) = (9 * 10^(9) * 5.9)/((0.042)^(2))`

=
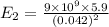
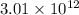`3.01 * 10^(12)` N (toward the positive x direction)

For the charge at y = 0.048 m

`E_(3) = (9 * 10^(9) * 2.9)/(0.048)^(2)}`

=
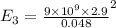
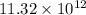`11.32 * 10^(12)` N (toward the negative y direction)

For the charge at y = 0.069 m

`E_(4) = (9 * 10^(9) * 8.2)/(0.069)^(2))`

=
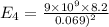
`15.50 * 10^(12)` N (toward the positive y)

Therefore, net x is calculated as follows.

The net x =
`3.01 * 10^(12) N - 3.01 * 10^(12) N`

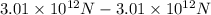
= 0 N

The net y =
`15.50 * 10^(12) N - 11.32 * 10^(12)` N

=
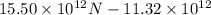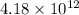`4.18 * 10^(12)` N (positive y)

Total net E is found by the pythagorean theorem as follows.

E =
`\sqrt{[(0 N)^(2) + (4.18 * 10^(12) N)^(2)]`

=
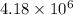`4.18 * 10^(6)` N

Thus, we can conclude that the net electric field (magnitude and direction) at the origin is
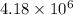`4.18 * 10^(6)` N.