Question

In a study relating the degree of warping, in mm, of a copper plate (y) to temperature in °C (x), the following summary statistics were calculated: n=40, x¯=26.36, y¯=0.5188,∑ni=1(xi−x¯)2=98,775, ∑ni=1(yi−y¯)2=19.4,∑ni=1(xi−x¯)(yi−y¯)=796.94. Compute the error sum of squares, the regression sum of squares, and the total sum of squares. Round the error sum of squares and regression sum of squares to three decimal places.

The error sum of squares is ______

The regression sum of squares is ______

The total sum of squares is _______

Answer 1

The error sum of squares is SSE=12.97

The regression sum of squares is SSR=6.430

The total sum of squares is SST=19.4

Explanation:

Linear regression is a way "to modeling the relationship between a scalar response (or dependent variable) and one or more explanatory variables (or independent variables)".

Regression estimates are "used to describe data and to explain the relationship between one dependent variable and one or more independent variables"

The linear model is given by the following equation
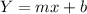`Y=mx +b`, where y is the dependent variable, x the independent variable, m the slope and b the intercept.

For this case we have the following info given:

`\sum_(i=1)^n (x_i -\bar x)^2 =98775`

`\sum_(i=1)^n (y_i -\bar y)^2 =19.4`

`\bar x =26.36`

`\bar y =0.5188`

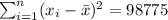
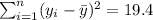
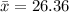
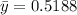
n= 40 represent the sample size

`\sum_(i=1)^n (x_i -\bar x)(y_i -\bar y) =796.94`

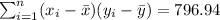
The total sum of squares is given by this formula:

`SST= \sum_(i=1)^n (y_i -\bar y)^2 =19.4`

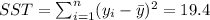
And from the formulas for a simple regression, we need to calculate the slope for the regression like this:

`m=(\sum_(i=1)^n (x_i -\bar x)(y_i -\bar y))/(\sum_(i=1)^n (x_i -\bar x)^2)`

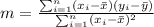
And if we replace the values given we have:

`m=(796.94)/(98775)=0.008068`

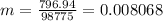
We have another useful equation in order to find the sum of squares for the regression, given by:

`SSR=m* \sum_(i=1)^n (x_i -\bar x)(y_i -\bar y)=0.008068*796.94=6.430`

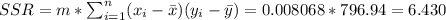
And we know this equivalence:

`SST= SSR+SSE`

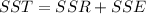
And solving for the sum of squares for the error we have:

`SSE=SST-SSR=19.4-6.430=12.97`

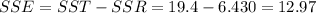
So then we have the final solutions:

The error sum of squares is SSE=12.97

The regression sum of squares is SSR=6.430

The total sum of squares is SST=19.4