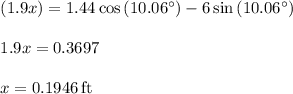Answer:
Part A-
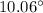
Part B- 0.1946ft
Step-by-step explanation:
Block A
Apply force equilibrium equation along x direction.
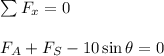
Here,
 } is friction force on block A and
} is friction force on block A and
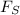 }is spring force, and \theta is inclination angle.
}is spring force, and \theta is inclination angle.
By substitution
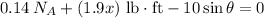
Similarly, apply force equilibrium equation along y direction.

By substitution

Block B
Apply force equilibrium equation along x direction.
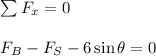
By substitution

Apply force equilibrium equation along y direction.

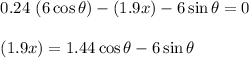
Calculate the inclination angle when both blocks begin to slide.
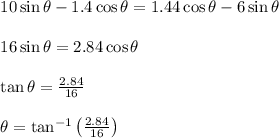
Calculate the change in length of the spring.