Answer:
- maximum: 9 at (x, y, z) = (1, 0, 0)
- minimum: 3 at (x, y, z) = (0, 0, 1)
Explanation:
The method of Lagrange multipliers can be used to find the extrema subject to the constraint. The Lagrangian can be written ...
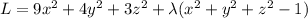
We want to find the solution to the simultaneous equations when the partial derivatives are all zero.
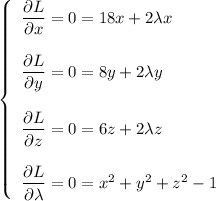
These can be simplified to ...

The first of these has solutions x=0 or λ=-9. In the latter case, the other equations require y=z=0 and x=1.
The second has solutions y=0 or λ=-4. In the latter case, the other equations require x=z=0 and y=1.
The third has solutions z=0 or λ=-3. In the latter case, the other equations require x=y=0 and z=1.
The objective function (given quadratic form) has these values at the points just found:
9 for (x, y, z) = (1, 0, 0) . . . . . a maximum
4 for (x, y, z) = (0, 1, 0)
3 for (x, y, z) = (0, 0, 1) . . . . . a minimum
_____
Alternate approach
You can solve the constraint for z^2 and substitute that into the objective function f(x, y, z). It will then be ...
f(x, y) = 9x^2 +4y^2 +3(1 -x^2 -y^2) = 6x^2 +3y^2 +3
Since x^2 and y^2 must be non-negative, the minimum value of this function is clearly 3.
Similarly, you can solve the constraint for x^2 and substitute that into f(x, y, z) to get ...
f(y, z) = 9(1 -y^2 -z^2) +4y^2 +3z^2 = -5y^2 -6z^2 +9
Again, the fact that y^2 and z^2 are zero at least means the maximum value of f(y, z) is 9.