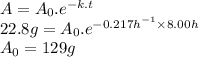Question

An unknown radioactive substance has a half-life of 3.20 hours . If 22.8 g of the substance is currently present, what mass A0 was present 8.00 hours ago? Express your answer with the appropriate units.

Answer 1

129 g

Step-by-step explanation:

The radioactive decay of a substance can be represented through the following expression.

`A=A_(0).e^(-k.t)`

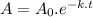
where,

A is the amount of A at certain time t

A₀ is the initial amount of A

k is the rate constant

We can find k from the half-life (t1/2) using the following expression.

`t_(1/2)=(ln2)/(k) \\k=(ln2)/(t_(1/2)) =(ln2)/(3.20h) =0.217h^(-1)`

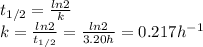
If 22.8 g of the substance is currently present, what mass A₀ was present 8.00 hours ago?

`A=A_(0).e^(-k.t)\\22.8g = A_(0).e^{-0.217h^(-1)* 8.00h} \\A_(0)=129g`