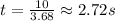Question

The sports car has a weight of 4500-lb and a center of gravity at G. If it starts from rest it causes the rear wheels to slip as it accelerates. Determine how long it takes for it to reach a speed of 10 ft/s. Also, what are the normal reactions at each of the four wheels on the road? The coefficients of static and kinetic friction at the road are us=0.5 and uk=0.3, respectively. Neglect the mass of the wheels.

Answer 1

Time=2.72 seconds

Front wheel reactions= 1393 lb

Rear wheel reactions= 857 lb

Step-by-step explanation:

The free body diagram is assumed to be the one attached here

The mass, m of the car is

`M=\frac {W}{g}` where W is weight and g is acceleration due to gravity

Taking g as
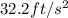`32.2 ft/s^(2)` then

`M=\frac {4500}{32.2}=139.75 lbm`

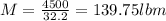
Considering equilibrium in x-axis

`Ma_G-f=0`

`Ma_G-(\mu_g* 2N_B)=0`

`139.75* a_G-(0.3* 2* N_B)=0`

`0.6N_B=139.75a_g`

`N_B=232.92a_g`

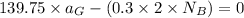
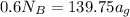
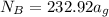
At point A using the law of equilibrium, the sum of moments is 0 hence

`-2N_B(6)+4500(2)=-Ma_G(2.5)`

`-12N_B+9000=-139.75a_G* 2.5`

`-12(232.92a_G)+900=-349.375a_G`

`a_g\approx 3.68 ft/s^(2)`

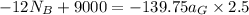
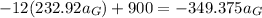
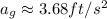
The normal reaction at B is therefore

`N_B=232.92a_G=232.92* 3.68\approx 857 lb`

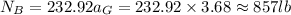
Consider equilibrium in y-axis

`4500-2N_A-2N_B=0`

`N_A+N_B=2250`

`N_A+857=2250`

`N_A=1393 lb`

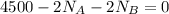
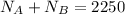
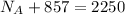
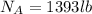
To find time that the car takes to a speed of 10 ft/s

Using kinematic equation

V=u+at

10=0+3.68t

`t=\frac {10}{3.68}\approx 2.72 s`