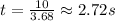Answer:
Time=2.72 seconds
Front wheel reactions= 1393 lb
Rear wheel reactions= 857 lb
Step-by-step explanation:
The free body diagram is assumed to be the one attached here
The mass, m of the car is
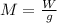 where W is weight and g is acceleration due to gravity
where W is weight and g is acceleration due to gravity
Taking g as
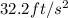 then
then
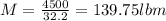
Considering equilibrium in x-axis

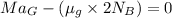
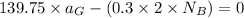
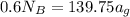
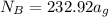
At point A using the law of equilibrium, the sum of moments is 0 hence
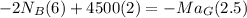
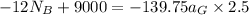
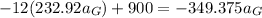
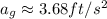
The normal reaction at B is therefore
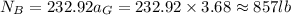
Consider equilibrium in y-axis
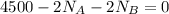
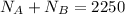
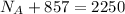
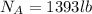
To find time that the car takes to a speed of 10 ft/s
Using kinematic equation
V=u+at
10=0+3.68t