Answer: The required probability is 0.07351.
Step-by-step explanation: Given that X is a binomial variable with n = 9 and p = 0.3.
We are given to compute the probability P(X = 5) and round the answer to five decimal places.
We know that
the binomial distribution formula for P(X = r) with n number of trials is given by
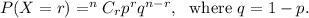
According to the given information, we have
n = 9, p = 0.3 and q = 1 - p = 1 - 0.3 = 0.7.
Therefore, we get
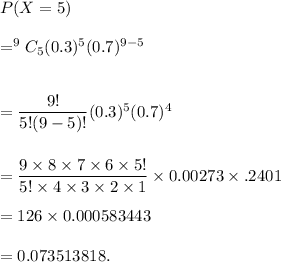
Rounding to five decimal places, we get
P(X=5) = 0.07351.
Thus, the required probability is 0.07351.