Question

Note: Enter your answer and show all the steps that you use to solve this problem in the space provided. Write and solve an equation for the situation. Eight and one-half years ago, Steven was 7 years old. How old is he now?

Please explain as they say.

Answer 1

Steven is 15 and one half years old now

Explanation:

Linear equations

Sometimes we need to know the value of a variable in a given equation and that variable is given as a polynomial of degree 1. Solving for that variable means isolating it and replacing the other known values

Steven was 7 years old eight and one-half years ago. If we call x as the actual age of Steven, his age eight and one-half years ago was

`x-8(1)/(2)`

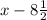
We know he was 7 years old then, so

`x-8(1)/(2)=7`

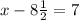
We need to know his actual age, so let's solve for x, adding
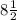`8(1)/(2)` to each side of the equation

`x-8(1)/(2)+8(1)/(2)=7+8(1)/(2)`

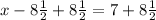
Simplifying

`x=15(1)/(2)`

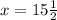
Steven is 15 and one half years old now