Answer:
1 hot dog costs $0.75
1 bratwurst costs $1.35
Explanation:
Let x and y be the price per dozen of hot dogs and bratwursts respectively.
The first day they sold 8 dozen hot dogs and 13 dozen bratwursts for $282.60
8x + 13y = 282.60
The second day they sold 10 dozen hot dogs and 15 dozen bratwursts for a total of $333.00
10x + 15y = 333
and we have the linear system
8x + 13y = 282.60
10x + 15y = 333
which can be written in matrix form as
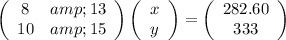
The solution would be given by
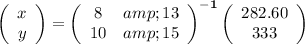
We have
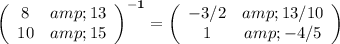
hence
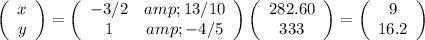
Now,
if a dozen hot dogs cost $9, 1 hot dog costs 9/12 = $0.75
if a dozen bratwursts cost $16.2, 1 bratwurst costs 16.2/12 = $1.35