Question

A turntable with a rotational inertia of 0.0120 kg∙m2 rotates freely at 2.00 rad/s. A circular disk of mass 200 g and radius 30.0 cm, and initially not rotating, slips down a spindle and lands on the turntable. (a) Find the new angular velocity. (b) What is the change in kinetic energy?

Answer 1

To solve this problem it is necessary to apply the related concepts to the moment of inertia in a disk, the conservation of angular momentum and the kinematic energy equations for rotational movement.

PART A) By definition we know that the moment of inertia of a disk is given by the equation

`I = (1)/(2) MR^2`

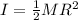
Where

M = Mass of the disk

R = Radius

Replacing with our values we have

`I = (1)/(2) (0.2)(0.3)^2`

`I = 9*10^(-3)kg\cdot m^2`

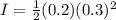
The initial angular momentum then will be given as

`I = I_1 \omega_1`

`I = 0.012*2`

`I = 0.024kg\cdot m^2/s`

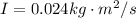
Therefore the total moment of inertia of the table and the disc will be

`I_2 = 9*10^(-3)+0.012`

`I_2 = 0.021kg\cdot m^2`

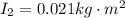
The angular velocity at the end point will be given through the conservation of the angular momentum for which it is understood that the proportion of inertia and angular velocity must be preserved. So

`I_1 \omega_1 = I_2\omega_2`

`(0.012)(2)=(1.08*10^(-4))\omega_2`

`\omega_2 = (0.012*2)/(0.021)`

`\omega_2 = 1.15rad/s`

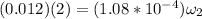
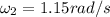
Therefore the new angular velocity is 1.15rad/s

PART B) Through the conservation of rotational kinetic energy we can identify that its total change is subject to

`\Delta KE = (1)/(2)I_1\omega_1^2-(1)/(2)I_2\omega^2`

`\Delta KE = (1)/(2)(I_1\omega_1^2-I_2\omega^2)`

`\Delta KE = (1)/(2)(0.024*2^2-0.021*1.15^2)`

`\Delta KE = 0.034J`

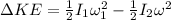
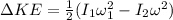
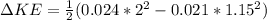
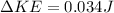
Therefore the change in kinetic energy is 0.034J