Question

The candy company that makes M&M's claims that 10% of the M&M's it produces is green. Suppose that the candies are packaged at random in large bags of 200 M&M's. When we randomly pick a bag of M&M's, we may assume that this represents a simple random sample of size n = 200. Suppose we wish to test H0: p = 0.10 versus Ha: p ≠ 0.10. Suppose that in the randomly selected bag of M&M's there are only 12 green M&M's. Calculate the value of the large-sample z statistic. If a 90% confidence interval were also calculated from the data, would it contain the value 0.10?

Answer 1

a)
`z=\frac{0.06-0.1}{\sqrt{(0.1(1-0.1))/(200)}}=-1.886`

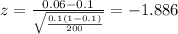
b) The 90% confidence interval would be given by (0.0324;0.0875)

So the confidence interval not contains the 0.1.

Explanation:

1) Data given and notation n

n=200 represent the random sample taken

X=12 represent the number of M&M's green

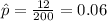`\hat p=(12)/(200)=0.06` estimated proportion of M&M's green.

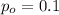`p_o=0.1` is the value that we want to test

`\alpha` represent the significance level

z would represent the statistic (variable of interest)

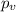`p_v` represent the p value (variable of interest)

2) Concepts and formulas to use

We need to conduct a hypothesis in order to test the claim that the true proportion of M&M's green is 0.1. The system of hypothesis are:

Null hypothesis:
`p=0.1`

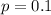
Alternative hypothesis:
`p \\eq 0.1`

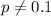
When we conduct a proportion test we need to use the z statistic, and the is given by:

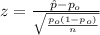`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

The One-Sample Proportion Test is used to assess whether a population proportion
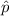`\hat p` is significantly different from a hypothesized value
`p_o`.

3) Calculate the statistic

Since we have all the info requires we can replace in formula (1) like this:

`z=\frac{0.06-0.1}{\sqrt{(0.1(1-0.1))/(200)}}=-1.886`

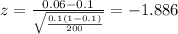
4) Statistical decision

P value method or p value approach . "This method consists on determining "likely" or "unlikely" by determining the probability assuming the null hypothesis were true of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed". Or in other words is just a method to have an statistical decision to fail to reject or reject the null hypothesis.

The significance level is not provided, but we can assume
`\alpha=0.05`. The next step would be calculate the p value for this test.

Since is a bilateral test the p value would be:

`p_v =2*P(z<-1.886)=0.059`

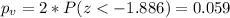
So based on the p value obtained and using the significance level assumed
`\alpha=0.05` we have
`p_v>\alpha` so we can conclude that we fail to reject the null hypothesis, and we can said that at 5% of significance the true proportion of M&M's green is not significantly different from 0.1 or 10% .

5) Confidence interval

In order to find the critical value we need to take in count that we are finding the interval for a proportion, so on this case we need to use the z distribution. Since our interval is at 90% of confidence, our significance level would be given by
`\alpha=1-0.90=0.1` and
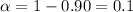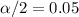`\alpha/2 =0.05`. And the critical values would be given by:

`t_(\alpha/2)=-1.64, t_(1-\alpha/2)=1.64`

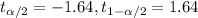
The confidence interval for the mean is given by the following formula:

`\hat p \pm z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}`

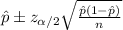
If we replace the values obtained we got:

`0.06 - 1.64\sqrt{(0.06(1-0.06))/(200)}=0.0324`

`0.06 + 1.64\sqrt{(0.06(1-0.06))/(200)}=0.0875`

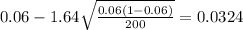
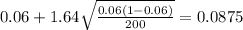
The 90% confidence interval would be given by (0.0324;0.0875)

So the confidence interval not contains the 0.1.