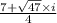Question

Help please!!!

Solve linear-quadratic system algebraically. Then what is the x coordinate of the solution? Show all work.

y – 5 = (x – 2)^2
x + 2y = 6

Answer 1

x =
`(7+√(47)* i )/(4)`

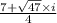
Explanation:

To solve quadratic systems,we always substitute one variable in terms if the other and then solve the equation.

x + 2y = 6 ---------------(1)

y - 5 =
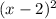`(x-2)^(2)` ---------------(2)

y =
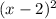`(x-2)^(2)` + 5 ---------------(3)

Substitute (3) in (1) ,

x + 2(
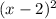`(x-2)^(2)` + 5 ) = 6

`(a + b)^(2)` =
`a^(2) + 2ab + b^(2)`

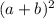x + 2(
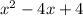`x^(2) - 4x + 4` + 5 ) = 6

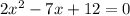`2x^(2) - 7x + 12=0` --------------(4)

The roots of the quadratic equation
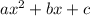`ax^(2)  +bx+c` is

x =
`\frac{(-b) + \sqrt{(-b)^(2)-4 * ac }  }{2 * a}` -----------(5)

According to equation (5),solution of (4) is

x =
`\frac{7 + \sqrt{(-7)^(2)-4 * 24 }  }{2 * 2}`

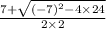
x =
`(7+√(49-96))/(4)`

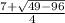
x =
`(7+√(47)* i )/(4)`