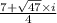Answer:
x =
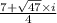
Explanation:
To solve quadratic systems,we always substitute one variable in terms if the other and then solve the equation.
x + 2y = 6 ---------------(1)
y - 5 =
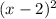 ---------------(2)
---------------(2)
y =
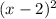 + 5 ---------------(3)
+ 5 ---------------(3)
Substitute (3) in (1) ,
x + 2(
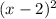 + 5 ) = 6
+ 5 ) = 6
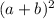 =
=
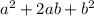
x + 2(
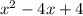 + 5 ) = 6
+ 5 ) = 6
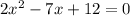 --------------(4)
--------------(4)
The roots of the quadratic equation
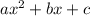 is
is
x =
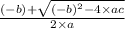 -----------(5)
-----------(5)
According to equation (5),solution of (4) is
x =
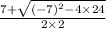
x =
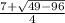
x =