Question

wo lacrosse players collide in midair. Jeremy has a mass of 120 kg and is moving at a speed of 3 m/s. Hans has a mass of 140 kg and is moving at a speed of –2 m/s. After the collision, they bounce away from each other, and Jeremy is moving at a speed of –2.5 m/s. How fast is Hans moving after the collision?

Answer 1

2.71 m/s fast Hans is moving after the collision.

Step-by-step explanation:

Given that,

Mass of Jeremy is 120 kg (
`M_J`)

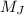Speed of Jeremy is 3 m/s (
`V_J`)

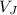Speed of Jeremy after collision is (
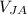`V_(JA)`) -2.5 m/s

Mass of Hans is 140 kg (
`M_H`)

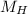Speed of Hans is -2 m/s (
`V_H`)

Speed of Hans after collision is (
`V_(HA)`)

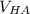Linear momentum is defined as “mass time’s speed of the vehicle”. Linear momentum before the collision of Jeremy and Hans is

=
`=\mathrm{M}_(1) * \mathrm{V}_{\mathrm{J}}+\mathrm{M}_{\mathrm{H}} * \mathrm{V}_{\mathrm{H}}`

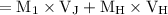
Substitute the given values,

= 120 × 3 + 140 × (-2)

= 360 + (-280)

= 80 kg m/s

Linear momentum after the collision of Jeremy and Hans is

=
`=\mathrm{M}_{\mathrm{J}} * \mathrm{V}_{\mathrm{JA}}+\mathrm{M}_{\mathrm{H}} * \mathrm{V}_{\mathrm{HA}}`

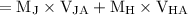
= 120 × (-2.5) + 140 ×
`V_(HA)`

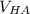
= -300 + 140 ×
`V_(HA)`

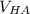
We know that conservation of liner momentum,

Linear momentum before the collision = Linear momentum after the collision

80 = -300 + 140 ×
`V_(HA)`

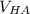
80 + 300 = 140 ×
`V_(HA)`

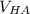
380 = 140 ×
`V_(HA)`

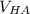
380/140=
`V_(HA)`

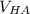
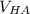`V_(HA)` = 2.71 m/s

2.71 m/s fast Hans is moving after the collision.