2.71 m/s fast Hans is moving after the collision.
Step-by-step explanation:
Given that,
Mass of Jeremy is 120 kg (
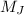 )
)
Speed of Jeremy is 3 m/s (
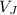 )
)
Speed of Jeremy after collision is (
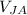 ) -2.5 m/s
) -2.5 m/s
Mass of Hans is 140 kg (
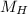 )
)
Speed of Hans is -2 m/s (
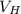 )
)
Speed of Hans after collision is (
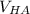 )
)
Linear momentum is defined as “mass time’s speed of the vehicle”. Linear momentum before the collision of Jeremy and Hans is
=
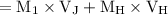
Substitute the given values,
= 120 × 3 + 140 × (-2)
= 360 + (-280)
= 80 kg m/s
Linear momentum after the collision of Jeremy and Hans is
=
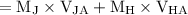
= 120 × (-2.5) + 140 ×
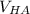
= -300 + 140 ×
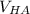
We know that conservation of liner momentum,
Linear momentum before the collision = Linear momentum after the collision
80 = -300 + 140 ×
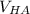
80 + 300 = 140 ×
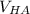
380 = 140 ×
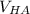
380/140=
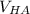
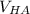 = 2.71 m/s
= 2.71 m/s
2.71 m/s fast Hans is moving after the collision.