Answer:
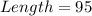 feet
feet
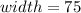 feet
feet
Explanation:
Let x be the width of a rectangle
Let l be the length of a rectangle
Let A be the area of rectangle
Given.
The garden is 20 feet longer than wide
therefore
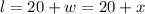
Area of rectangle is
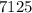
We know that area of rectangle is
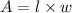 ---------------------(1)
---------------------(1)
put all known values in equation 1
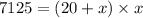

Find roots of equation by this formula
where

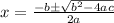
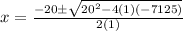

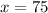 or
or
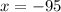
check both value in equation 1
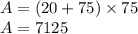
So, the
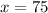 is satisfy the equation 1.
is satisfy the equation 1.
So The length of rectangle =
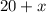 =
=
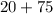 =
=
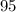 feet
feet
And width is 75 feet