Question:
A right rectangular prism's edge lengths are
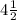 inches, 4 inches, and 3 inches. How many unit cubes with edge lengths of
inches, 4 inches, and 3 inches. How many unit cubes with edge lengths of
 inch can fit inside the prism?
inch can fit inside the prism?
Answer:
1458 cubes with edge lengths of
 inch can fit inside the prism.
inch can fit inside the prism.
Explanation:
Given:
Dimensions of the rectangular prism =
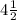 inches, 4 inches, and 3 inches
inches, 4 inches, and 3 inches
length of Edge of the cube =

To Find:
Number of unit cubes that can fit inside the prism =?
Solution:
Step 1: Finding the volume of the right rectangular prism
Volume of the right Rectangular prism is =

where
w = width of theright Rectangular prism
h = height of the right Rectangular prism
l = lenght of the right Rectangular prism
Substituting the values ,
Volume of the right Rectangular prism is =
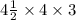
Volume of the right Rectangular prism is =
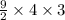
Volume of the right Rectangular prism is =
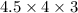
Volume of the right Rectangular prism is = 54
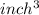
Step 2: Finding the volume of the cube
Volume of the cube =
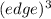
Substituting the values,
Volume of the cube =
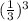
Volume of the cube =

Step 3: Find the number of cube that can fit in the cube.
Number of cubes =
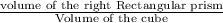
Number of cubes =
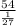
Number of cubes =

Number of cubes = 1458 cubes