Question

A vendor sells h hot dogs and s sodas. If a hot dog costs twice as much as a soda, and if the vendor takes in a total of d dollars, how many cents does a soda cost?

Answer 1

The expression for the cost of soda is 100 ×
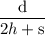`(\textrm d)/( \textrm 2h + \textrm s)` cents

Explanation:

Given as :

The quantity of hot dogs sold by vendor = h

The quantity of sodas sold by vendor = s

The total cost of hot dogs and soda = $ d

Let The price of hot dogs = $ x

And The price of soda = $ y

Now, According to question

The price of hot dogs is twice as much as soda

so, $ x = 2 × $ y

I.e x = 2 y

and $ x h + $ y s = $ d

Or , 2 × $ y h + $ y s = $ d

Or, y =
`(\textrm d)/( \textrm 2h + \textrm s)`

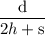
∵ 1 dollar = 100 cents

So, the price of
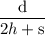`(\textrm d)/( \textrm 2h + \textrm s)` = 100 ×
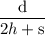`(\textrm d)/( \textrm 2h + \textrm s)` cents

Hence The expression for the cost of soda is 100 ×
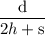`(\textrm d)/( \textrm 2h + \textrm s)` cents Answer