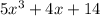Answer:
Part I: The degree of a polynomial is the greatest of the degrees of its terms.
Part II: In order to write a polynomial in descending order, you must write the terms with the exponents decreasing from left to right.
Part III: A. -4x² + 11x - 12, degree = 2,
B. 5x³ + 4x + 14, degree = 3.
Explanation:
Part I : Since, the degree of a polynomial is the highest power of its monomials ( single term ),
eg : degree of
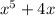 is 5.
is 5.
Thus, in part I, the correct option is 'greatest'
Part II : When we write a polynomial then we write the terms of the polynomial in descending order of their degrees.
Thus, in part II the correct option is 'least'
Part III : A.
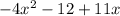
∵ -4x² has the highest power in the polynomial.
⇒ Degree = 2,
Also, in the polynomial descending order of degrees,
2 > 1 > 0
⇒ polynomial in descending order,
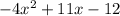
B.
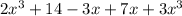
Combining like terms,
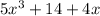
∵ 5x³ has the highest degree,
⇒ Degree = 3,
Also, the order of the degrees in the polynomial is,
3 < 2 < 1 < 0
Thus, the polynomial in descending order,