Question

The area of the figure

Answer 1

The Area of Δ TOP is 43.55 units².

Explanation:

Given:

P ≡ ( x₁ ,y₁ ) ≡ ( -5 , -7)

T ≡ ( x₂ ,y₂ ) ≡ ( 1 , 8)

O ≡ ( x₃ ,y₃ ) ≡ ( 6 , 6)

To Find :

Area of Δ TOP = ?

Solution :

We have

`\textrm{Area of Triangle TOP} = (1)/(2)* Base* Height\\\textrm{Area of Triangle TOP} = (1)/(2)* OT* PT`

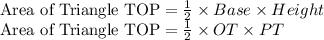
Now Distance formula we have

`l(PT) = \sqrt{((x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2) )}`

`l(OT) = \sqrt{((x_(3)-x_(2))^(2)+(y_(3)-y_(2))^(2) )}`

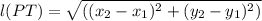
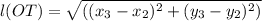
Substituting the given values we get

`l(PT) = \sqrt{((1--5)^(2)+(8--7)^(2) )}\\l(PT) = \sqrt{((1+5)^(2)+(8+7)^(2) )}\\l(PT) = \sqrt{((6)^(2)+(15)^(2) )}\\l(PT) = √(261)\\l(PT) = 16.16\ units`

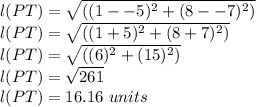
And

`l(OT) = \sqrt{((x_(3)-x_(2))^(2)+(y_(3)-y_(2))^(2) )}\\l(OT) = \sqrt{((6-1)^(2)+(6-8)^(2) )}\\l(OT) = \sqrt{((5)^(2)+(-2)^(2) )}\\l(OT) = √(29)\\l(OT) = 5.39\ units`

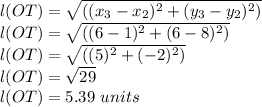
Now substituting OT and PT in area formula we get

`\textrm{Area of Triangle TOP} = (1)/(2)* 5.39* 16.16\\\textrm{Area of Triangle TOP} = 43.55\ units^(2)`

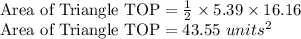
Therefore, Area of Δ TOP is 43.55 units².