Question

A 50.0 mL sample containing Cd2+ and Mn2+ was treated with 58.4 mL of 0.0400 M EDTA . Titration of the excess unreacted EDTA required 15.9 mL of 0.0130 M Ca2+ . The Cd2+ was displaced from EDTA by the addition of an excess of CN− . Titration of the newly freed EDTA required 22.4 mL of 0.0130 M Ca2+ . What are the concentrations of Cd2+ and Mn2+ in the original solution?

Answer 1

[Cd²⁺] = 5.82x10⁻³ M

[Mn²⁺] = 0.037M

Step-by-step explanation:

The titration of EDTA with Cd²⁺, Mn²⁺ and Ca²⁺ are based in the formation of complexes with a relation 1:1, EDTA: metal, so from the titration of the excess unreacted EDTA with Ca²⁺ we can calculate the EDTA moles by:

`\eta_(EDTA)_(e) = \eta_(Ca^(2+))`

`\eta_(EDTA)_(e) = 15.9 \cdot 10^(-3) L \cdot 0.0130M = 2.07 \cdot 10^(-4) moles`

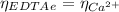
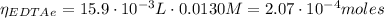
The moles of EDTA are:

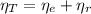`\eta_(T) = \eta_(e) + \eta_(r)` (1)

where
`\eta_(T)`: is the total moles of EDTA,
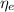`\eta_(e)`: is the EDTA excess moles and
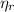`\eta_(r)`: is the EDTA moles that react with Cd²⁺ and Mn²⁺

Hence the EDTA moles that react with Cd²⁺ and Mn²⁺ are equal to the moles of both metals:

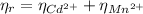`\eta_(r) = \eta_(Cd^(2+)) + \eta_(Mn^(2+))` (2)

From equation (1) we can find the
`\eta_(r)`:

`\eta_(r) = \eta_(T) - \eta_(e)`

`\eta_(r) = 58.4 \cdot 10^(-3)L \cdot 0.0400M - 2.07 \cdot 10^(-4) moles = 2.13 \cdot 10^(-3) moles`

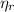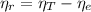
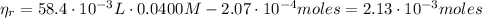
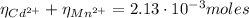`\eta_(Cd^(2+)) + \eta_(Mn^(2+)) = 2.13 \cdot 10^(-3) moles` (3)

Now, from the titration of the EDTA free of Cd²⁺ with Ca²⁺, we can calculate the moles of EDTA that react with the Cd²⁺ and hence the Cd²⁺ moles:

`\eta_(EDTA) = \eta_(Ca^(2+)) = 22.4 \cdot 10^(-3)L \cdot 0.0130M = 2.91 \cdot 10^(-4) moles`

`\eta_(Cd^(2+)) = 2.91 \cdot 10^(-4) moles`

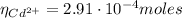
Having the Cd²⁺ moles we can now calculate the Mn²⁺ moles using equation (3):

`\eta_(Mn^(2+)) = 2.13 \cdot 10^(-3) moles -\eta_(Cd^(2+))`

`\eta_(Mn^(2+)) = 2.13 \cdot 10^(-3) moles - 2.91 \cdot 10^(-4) moles = 1.84 \cdot 10^(-3) moles`

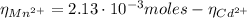
Now, with the Cd²⁺ moles and Mn²⁺ moles we can find their concentrations in the original solution:

`[Cd^(2+)] = (2.91 \cdot 10^(-4) moles)/(50.0\cdot 10^(-3)L) = 5.82 \cdot 10^(-3) M`

`[Mn^(2+)] = (1.84 \cdot 10^(-3) moles)/(50.0\cdot 10^(-3)L) = 0.037M`

I hope it helps you!