Question

YOU DON'T HAVE TO ANSWER ALL OF THEM SO PLEASE HELP ME ON QUESTION A PLEASE

The fee for taxi cab is $2.50 per passenger and $0.50 for each mile. A group of friends has $22.50 for cab fare.

a. Write a linear inequality to represent how many miles, y, the group can travel if there are x people in the group.

b. If there are 6 people in the group, what is the furthest they can travel with their budget?

c. If the group wants to travel 15 miles, what is the greatest number of passengers that can travel by taxi?

Answer 1

Part A

Answer: The inequality would be
`2.50x + 0.50y \le 22.50`

-------------

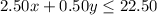
Step-by-step explanation:

x = number of people

2.50x = total cost of $2.50 per passenger, there are x passengers

y = number of miles

0.50y = total cost traveling y miles at $0.50 per mile

2.50x + 0.50y = grand total cost of everything mentioned so far

we want the grand total to be 22.50 or less, as this is the max budget. So that's why I set 2.50x+0.50y to be less than or equal to 22.50

============================================

Part B

Answer: 15 miles

------------

Step-by-step explanation:

We have x = 6 people so we have

`2.50x + 0.50y \le 22.50`

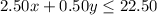
update to

`2.50(6) + 0.50y \le 22.50`

`15 + 0.50y \le 22.50`

`0.50y \le 22.50-15`

`0.50y \le 7.50`

`y \le (7.50)/(0.50)`

`y \le 15`

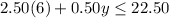
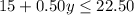
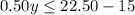
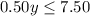
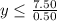
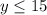
If there are 6 people, then the furthest they can travel is 15 miles. This is because y = 15 is the largest y value possible.

============================================

Part C

Answer: 6 passengers

-----------------

Step-by-step explanation:

This is just part B, just in reverse. Plug y = 15 into the inequality, then isolate x. You should find that
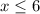`x \le 6`. There isnt much need to do much work here because part B effectively gives two pieces of information at once, so to speak.