Answer:
P(X≥520) =0.02938
Explanation:
given,
n = 1000
Population size = N = 2,000,000
Specified characteristic = P = 0.49
Probability of obtaining x = 520
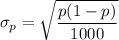
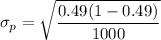
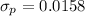
for x = 520
p = 520/1000 = 0.52
P(X≥520) = P(p≥0.52)
P(p≥0.52) =
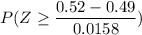
P(p≥0.52) =
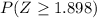
using z-table
P(p≥0.52) = 0.02938
P(X≥520) =0.02938