Answer with explanation:
Let p denotes the population proportion of all adult Americans who watched streamed programming up to that point in time.
Given : The Harris poll reported on November 13, 2012, that 53% of 2343 American adults surveyed said they have watched digitally streamed TV programming on some type of devices.
i.e. sample size :n= 2343
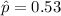
We know that ,
Critical value for 99% confidence interval =
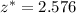
a) Confidence interval for population proportion:-
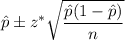

i.e. Confidence interval : (0.5035, 0.5565)
Interpretation: A person can be 99% confident that the true proportion of all adult Americans who watched streamed programming up to that point in time lies between 0.5035 and 0.5565 .
b) Margin of error : E= half of width of CI=
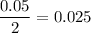
The formula to find the sample size , if the prior estimate of population proportion is known:

Put all the value in the above formula :

Thus , the minimum sample size = 2645