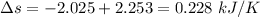Question

An aluminum block weighing 28 kg initially at 140°C is brought into contact with a block of iron weighing 36 kg at 60°C in an insulated enclosure. Determine the final equilibrium temperature and the total entropy change for this process. The specific heat of aluminum at 400 K is cp = 0.949 kJ/kg·K. The specific heat of iron at room temperature is cp = 0.45 kJ/kg·K. The final equilibrium temperature is K. The total entropy change for this process is kJ/K.

Answer 1

Equilibrium Temperature is 382.71 K

Total entropy is 0.228 kJ/K

Solution:

As per the question:

Mass of the Aluminium block, M = 28 kg

Initial temperature of aluminium,
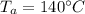`T_(a) = 140^(\circ)C` = 273 + 140 = 413 K

Mass of Iron block, m = 36 kg

Temperature for iron block,
`T_(i) = 60^(\circ)C` = 273 + 60 = 333 K

At 400 k

Specific heat of Aluminium,
`C_(p) = 0.949\ kJ/kgK`

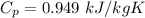
At room temperature

Specific heat of iron,
`C_(p) = 0.45\ kJ/kgK`

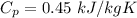
Now,

To calculate the final equilibrium temperature:

Amount of heat loss by Aluminium = Amount of heat gain by Iron

`MC_(p)\Delta T = mC_(p)\Delta T`

`28* 0.949(140 - T_(e)) = 36* 0.45(T_(e) - 60)`

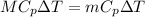
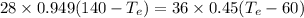
Thus

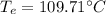`T_(e) = 109.71^(\circ)C` = 273 + 109.71 = 382.71 K

where

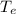`T_(e)` = Equilibrium temperature

Now,

To calculate the changer in entropy:

`\Delta s = \Delta s_(a) + \Delta s_(i)`

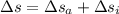
Now,

For Aluminium:

`\Delta s_(a) = MC_(p)ln(T_(e))/(T_(i))`

`\Delta s_(a) = 28* 0.949* ln(382.71)/(413) = - 2.025\ kJ/K`

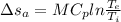
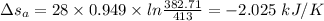
For Iron:

`\Delta s_(i) = mC_(i)ln(T_(e))/(T_(i))`

`\Delta s_(a) = 36* 0.45* ln(382.71)/(333) = 2.253\ kJ/K`

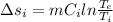
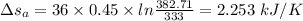
Thus

`\Delta s =-2.025 + 2.253 = 0.228\ kJ/K`