Answer:
a) Is a one tailed left test.
b) Null hypothesis: There is no difference between new and other toothpastes in the mean number of cavities of the general population
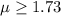
Alternative hypothesis : New toothpaste reduces cavities compared to other brands

c)

d)
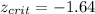
e)
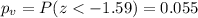
If we compare the p value and the significance level for example
 we see that
we see that
 so we can conclude that we have enough evidence to FAIL to reject the null hypothesis, so we can conclude that the mean number of cavities at a 6-month checkup is not significantly lower than 1.73 at 5% of significance.
so we can conclude that we have enough evidence to FAIL to reject the null hypothesis, so we can conclude that the mean number of cavities at a 6-month checkup is not significantly lower than 1.73 at 5% of significance.
f) The 95% confidence interval would be given by (1.217;1.783)
Explanation:
1) Data given and notation
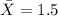 represent the mean annual premium value for the sample
represent the mean annual premium value for the sample
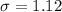 represent the population standard deviation
represent the population standard deviation
 sample size
sample size
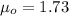 represent the value that we want to test
represent the value that we want to test
 represent the significance level for the hypothesis test.
represent the significance level for the hypothesis test.
z would represent the statistic (variable of interest)
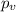 represent the p value for the test (variable of interest)
represent the p value for the test (variable of interest)
State the null and alternative hypotheses.
a) Is this a one- or two-tailed test?
Is a one tailed left test.
b) What are H0 and Ha for this study?
Null hypothesis: There is no difference between new and other toothpastes in the mean number of cavities of the general population
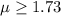
Alternative hypothesis : New toothpaste reduces cavities compared to other brands

c) Compute zobt
The statistic for this case is given by:
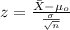 (1)
(1)
z-test: "Is used to compare group means. Is one of the most common tests and is used to determine if the mean is (higher, less or not equal) to an specified value".
Calculate the statistic
We can replace in formula (1) the info given like this:

d) What is zcv?
In order to find the critical value we need to find a value on the normal standard distribution such that:
 where 0.05 represent the significance level selected.
where 0.05 represent the significance level selected.
And this value is
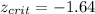
e) Should H0 be rejected? What should the researcher conclude?
Since is a one side left tailed test the p value would be:
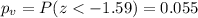
Conclusion
If we compare the p value and the significance level for example
 we see that
we see that
 so we can conclude that we have enough evidence to FAIL to reject the null hypothesis, so we can conclude that the mean number of cavities at a 6-month checkup is not significantly lower than 1.73 at 5% of significance.
so we can conclude that we have enough evidence to FAIL to reject the null hypothesis, so we can conclude that the mean number of cavities at a 6-month checkup is not significantly lower than 1.73 at 5% of significance.
f) Determine the 95% confidence interval for the population mean, based on the sample mean
The confidence interval for the mean is given by the following formula:
 (1)
(1)
Since the Confidence is 0.95 or 95%, the value of
 and
and
 , and we can use excel, a calculator or a tabel to find the critical value. The excel command would be: "=-NORM.INV(0.025,0,1)".And we see that
, and we can use excel, a calculator or a tabel to find the critical value. The excel command would be: "=-NORM.INV(0.025,0,1)".And we see that
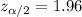
Now we have everything in order to replace into formula (1):
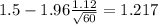
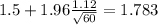
So on this case the 95% confidence interval would be given by (1.217;1.783)