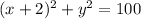The standard form of the equation of the circle with its center at (-2,0), and a radius of 10 is
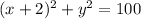
Solution:
We have been given the center of a circle and radius which are (-2,0) and 10 respectively
To find: Standard form of the equation of the circle
The standard form for the equation of a circle is given as:
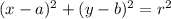
Where (a, b) are the coordinate of the centre of circle and r is the radius
Now on substituting values we get,
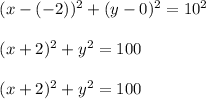
So, the required standard equation of circle is :-