Answer:
Option C.
Explanation:
Assume that the below figure attached with this question.
Distance formula:
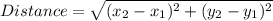
From the below figure it is clear that the vertices of triangle are A(-1,6), B(-1,1) and C(2,2).
Using distance formula we get
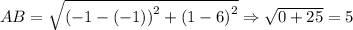
Similarly,
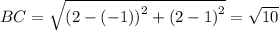
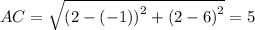
The perimeter of △ABC is
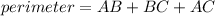
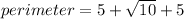
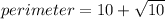
The perimeter of △ABC is
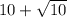 .
.
Therefore, the correct option is C.