Question

Shortest Distance from a Point to a Line-

Write an equation for the parabola with vertex at (3,-5) and going through (1,-8)

Answer 1

The equation of parabola in vertex form is
`y=(-3)/(4)(x-3)^(2)-5`

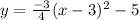
Solution:

Given that parabola with vertex (3, -5) and going through point (1, -8)

To find : equation of parabola

The equation of parabola in vertex form is given as:

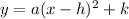`y=a(x-h)^(2)+k` ----- eqn 1

where (h, k) are the coordinates of the vertex

here (h, k) = (3, −5)

Substituting the values in above formula, we get

`y=a(x-3)^(2)+(-5)`

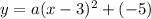
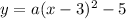`y=a(x-3)^(2)-5` ----- eqn 2

The given equation of parabola passes through (1, -8)

Substituiting (x, y) = (1, -8) in eqn 2 we get,

`\begin{array}{l}{-8=a(1-3)^(2)-5} \\\\ {-8=a(-2)^(2)-5} \\\\ {-8=a * 4-5} \\\\ {-8+5=4 a} \\\\ {-3=4 a} \\\\ {a=(-3)/(4)}\end{array}`

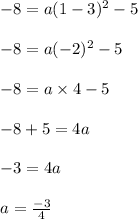
Now substitute the value of "a" in eqn 2,

`y=\left((-3)/(4)\right)(x-3)^(2)-5`

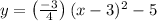
Thus the equation of parabola in vertex form is found